Quantum Cascade Laser
Figure of Merit Derivation
1 Figure of merit the easy way
The figure of merit (FoM) for a quantum cascade (QC) laser (QCL) is a tool used to maximize performance from a QC design. The FoM represents the parameters from the QC laser gain coefficient that are affected by the quantum design of a QC structure. The QCL gain coefficient is generally given as:
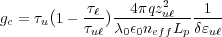 | (1) |
where τu is the lifetime of the upper laser state, τℓ is the lifetime of the lower laser state, q is the electron charge, τuℓ is the transition time between the upper and
lower laser state, zuℓ is the optical dipole matrix element (having
units of length), λ0 is the free space wavelength of the lasing
transition, neff is the effective refractive index of the optical
mode, Lp is the length of a single active-injector region
period, and δɛuℓ is the full-width-at-half-maximum (FWHM) of
transition’s spontaneous emission (usually taken as the measured FWHM of a QC
structure’s electroluminescence, and in units of energy). The gain coefficient
as defined this way has units of 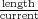 , which is generally
, which is generally
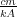 .
.
Since the optical dipole matrix element zuℓ and the energy state lifetimes τi are QC design-dependent parameters, the most direct approach to deriving a FoM is simply to pull these factors from the gain coefficient.
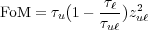 | (2) |
Thus, the FoM has units of time x length2; the standard units are ps Å2. While this is the simplest method for deriving a FoM, it has severe limitations when practically implemented. QC lasers after all, comprise a system of coupled quantum wells with significant intermixing (anticrossing) of quantum states; in Eq. (2), we have assumed only a single upper laser state and a single lower laser state.
2 Intermixed lower energy states
For a proper calculation of the laser gain coefficient—and thus FoM—we must include all optical transitions that might contribute photons into the lasing mode. One might address this problem by perturbing the field at which the FoM parameters are calculated, so as to prevent the upper and lower laser states from intermixing with nearby states. However, the FoM itself is a field-dependent parameter, so this approach is not ideal for calculating laser gain at current turn-on (i.e., the design field).
To more broadly address the problem of multiple charge carrier transitions contributing photons to the lasing mode, we need to consider each potential transition’s contribution to the optical gain. As an example, let’s examine an optical transition with one upper energy state and two closely spaced, intermixed lower energy states.

We need to remember that each transition has
its own spontaneous emission spectrum with a finite FWHM; in intersubband
heterostructure emitters, a good estimate for δɛuℓ is 10% of the transition energy. If the two
transitions are close enough together, the spontaneous emission will overlap
in energy. Let’s assume the spontaneous emission lineshape 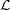 for a transition with
energy ɛuℓ has a Lorentzian form.
for a transition with
energy ɛuℓ has a Lorentzian form.
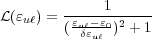 | (3) |
Here, ɛ0 is the lasing photon energy. Now, each transition
will be able to contribute to lasing. The lasing wavelength would not be exactly
that of a single optical transition, but somewhere between the two transitions.
To find the lasing wavelength, we need to keep in mind that the transitions
might have different spontaneous emission rates. That is, one transition might
be able to emit photons faster than the other. The spontaneous emission rate Wsp [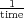 ] is the inverse of the
spontaneous emission lifetime τsp [time].
] is the inverse of the
spontaneous emission lifetime τsp [time].
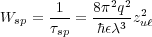 | (4) |
Notice that the rate, or the strength of the transition, is proportional to zuℓ2. If we add up the spontaneous emission spectrum of each transition multiplied by zuℓ2, the peak gain and thus the lasing energy ɛ0 can be found.
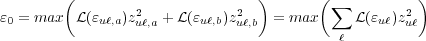 | (5) |
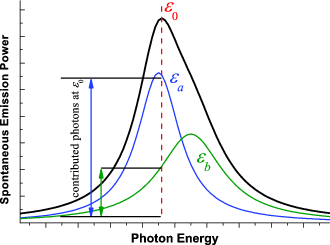
Now that we know what the lasing energy is
going to be, let’s look at stimulated emission for each of the transitions.
Gain γ [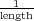 ] is simply the charge carrier population
difference N = Nu - Nℓ [
] is simply the charge carrier population
difference N = Nu - Nℓ [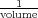 ] times the transition cross-section σ
[area].
] times the transition cross-section σ
[area].
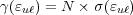 | (6) |
Let’s take each of the two contributions to γ individually. In a simple two level optical transition
system with an upper state pumped at rate Ru [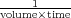 ], the carrier population
difference is
], the carrier population
difference is
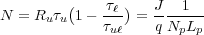 | (7) |
where J is pumping current density [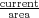 ] and Np is the number of active region-injector periods in
the QCL active core. The transition cross-section can be found by recognizing
that, at threshold where optical gain clamps,
] and Np is the number of active region-injector periods in
the QCL active core. The transition cross-section can be found by recognizing
that, at threshold where optical gain clamps,
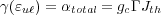 | (8) |
where αtotal is the total optical loss (waveguide and
mirror loss), Γ is the gain region confinement factor for the optical mode in
the waveguide, and Jth is the threshold current density [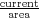 ]. By applying
Eqs. (1), (6) and (7) to Eq. (8), we get
]. By applying
Eqs. (1), (6) and (7) to Eq. (8), we get
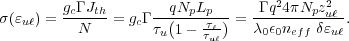 | (9) |
While this is close for the gain cross-section, we’ve got one correction to
make. The gain coefficient from Eq. (1) was derived assuming two
discreet states. To correct for this, we need to multiply the original gc by our lineshape function
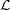 (ɛuℓ) from Eq. (3). Thus, we get the
quantum cascade laser transition cross-section.
(ɛuℓ) from Eq. (3). Thus, we get the
quantum cascade laser transition cross-section.
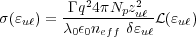 | (10) |
Now, getting back to our example with one upper energy state and two closely spaced lower energy states, we can pull from the components of Eq. (6) those elements that are influenced by quantum design.
| FoM | = τu 1 - 1 -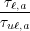  zuℓ,a2 zuℓ,a2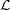 (ɛ
uℓ,a) + τu (ɛ
uℓ,a) + τu 1 - 1 -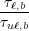  zuℓ,b2 zuℓ,b2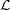 (ɛ
uℓ,b) (ɛ
uℓ,b) | ||
= ∑
ℓτu 1 - 1 -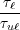  zuℓ2 zuℓ2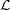 (ɛ
uℓ) (ɛ
uℓ) | (11) |
3 Intermixed upper energy states
Calculating a proper FoM for energy transitions with upper state intermixing takes consideration similar to the lower state intermixing case. However, with upper state intermixing, we have an additional complication. We cannot assume that each upper energy state is equally populated with electrons; the relative populations of each upper state will influence the total gain contributed by that transition.
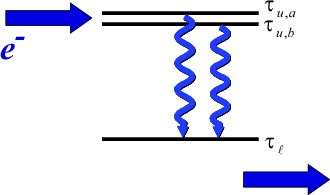
Recall that our basic relation for gain,
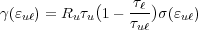 | (12) |
has a term Ru that describes the rate at which the upper energy level u is populated with electrons. For a FoM calculation, where we are focused on obtaining a number that allows us to compare different QC designs, we are not concerned about the absolute pumping rate. Rather, what we need is a weighting factor that reflects the relative population of each of the upper energy states. Now, we can write our FoM as
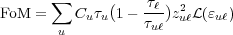 | (13) |
with an upper state weighting factor Cu. As we’ve previously shown, the pumping rate Ru of an energy state is proportional to the current density passing through the state. In a QCL system with strong coupling between energy states,
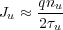 | (14) |
where nu is the sheet density [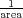 ] of electrons populating the state. Thus,
our weighting factor Cu ∝ nu∕τu. The energy state population nu follows the Fermi-Dirac distribution
] of electrons populating the state. Thus,
our weighting factor Cu ∝ nu∕τu. The energy state population nu follows the Fermi-Dirac distribution
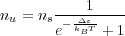 | (15) |
where Δɛ = ɛu -ɛF is approximately the energy difference between the state u and the injector ground state, kB is the Boltzmann constant, and T is temperature. For most quantum cascade laser systems, with relatively low doping (carrier densities) and high temperatures, the Fermi distribution is well-approximated by the Boltzmann distribution, so
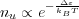 | (16) |
and
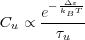 | (17) |
Since Cu is a weighting factor, the restriction ∑ uCu = 1 must hold.
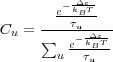 | (18) |
Finally, we arrive at the general equation for FoM by combining Eqs. (11) and (13), the generalized cases for transitions between intermixed upper and lower energy states.
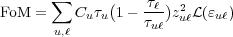 | (19) |